Data Sufficiency

Answer Choices on GMAT Data Sufficiency
DS questions always present the same five answer choices. In order to save time, it is best to memorize these answer choices rather than read them each time you face a DS question. A helpful acronym by which to memorize the answers is 12TEN.
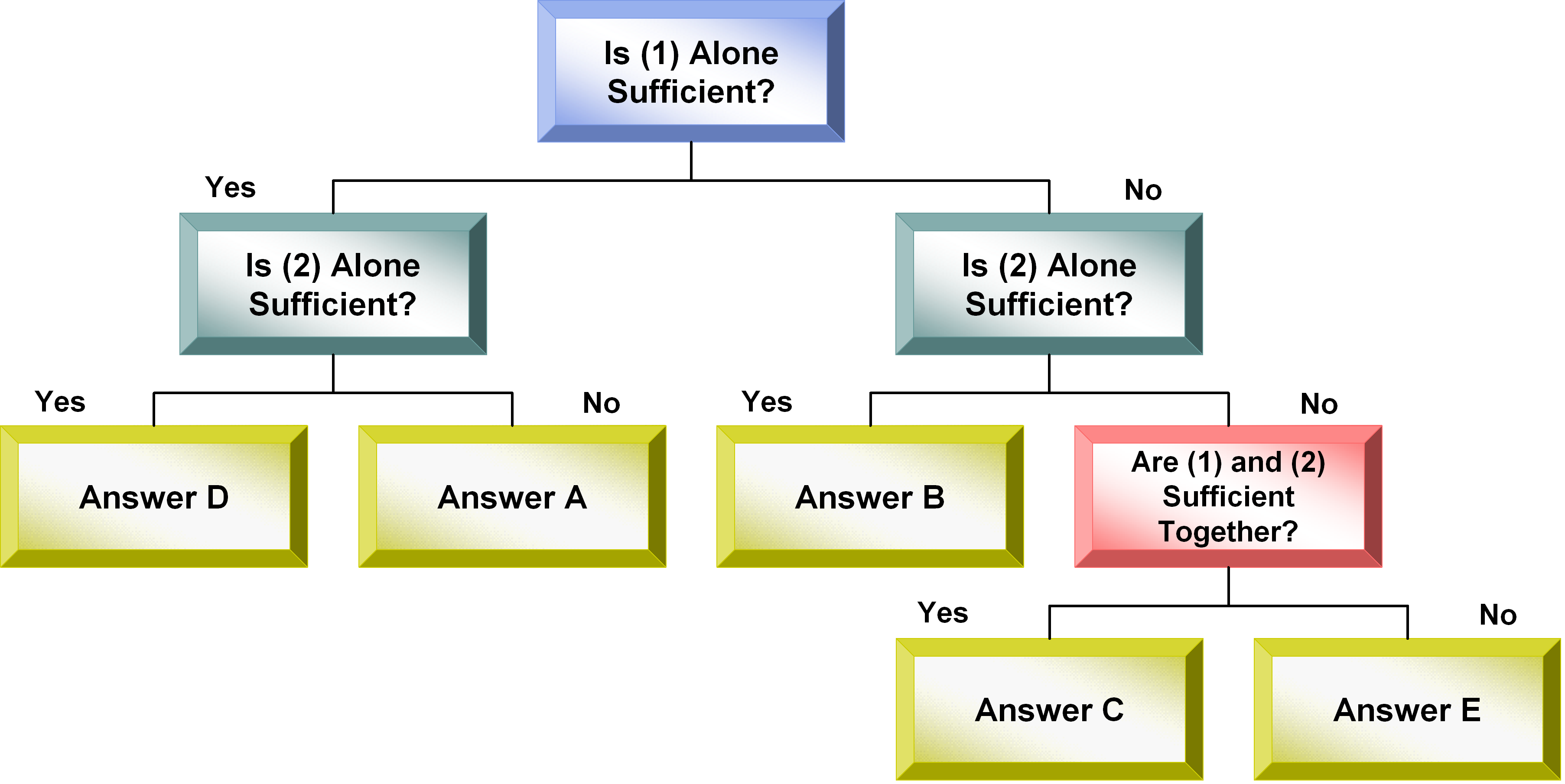
(A) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
(B) Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
(C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
(D) EACH statement ALONE is sufficient.
(E) Statements (1) and (2) TOGETHER are not sufficient.
In evaluating whether the statements provide sufficient information, you should first consider the information in (1), without taking the information in (2) into account. Then you should consider the information in (2), making sure to ignore the information in (1) that you just evaluated. Only if (1) by itself is not sufficient and (2) by itself is not sufficient, you should then evaluate sufficiency using (1) and (2) in combination. Consider the following answer elimination flowchart:
How to Approach GMAT Data Sufficiency
- For numerical value questions (e.g. What is the value of x?), you must be able to derive one exact number (e.g. x = 37) to have sufficient information. If you could come up with multiple numbers or a range of values, you do not have sufficient information.
- As the name implies, Yes/No questions (e.g. Does x = 37?) can be answered only with a yes and/or a no (e.g. yes, x does equal 37). For these questions, you must be able to answer definitely yes or definitely no to have sufficient information.
- The often-faster, more theoretical approach entails offering a mathematical justification. For example, one general algebraic principle is that if you have an equal number of unique linear equations as you have unknowns, then you can solve for the unknowns. In this case, you do not actually have to solve out the equations; merely knowing that you could solve them and derive a unique answer is all that matters.
- A second approach entails plugging in numbers. You try different numbers that meet any given constraints to check whether those different numbers could yield different answers or always yield the same answer to the question asked.
Sample GMAT Data Sufficiency Problem
Explanation to Problem
Answer: C
Since this question involves addition and multiplication of odd and even integers, it’ll be helpful to first review the relevant rules. In case we don’t remember one of these rules, we can easily verify by trying simple numbers. For example, since 2 + 1 = 3, we know that even + odd = odd.
| Even + Odd = Odd Odd + Even = Odd Even + Even = Even Odd + Odd = Even |
Even x Odd = Even Odd x Even = Even Even x Even = Even Odd x Odd = Odd |
The question asked is a Yes/No question. If the answer is always yes or always no, then we have sufficient information. If we can come up with a yes and a no answer, we do not have sufficient information. Let’s start by evaluating (1).
This immediately seems unlikely to be sufficient, because we don’t know much about b or c. But let’s try two cases to validate:
| Case 1: | Let’s say that b and c are both odd. Then we have (odd + odd) x (odd + odd) = (even) x (even) = even. So, answering the original question, do we have an even integer? YES |
| Case 2: | Since our first case yielded an even integer, we now want to check whether it’s possible to get an odd integer. This only happens if we have odd x odd. So how can we get odd times odd? What if b is odd and c is even. Then we have (odd + even) x (odd + even) = (odd) x (odd) = odd. So, answering the original question, do we have an even integer? NO |
Since we have a NO case and a YES case, (1) is not sufficient. Using our answer elimination flowchart, we know that answers A and D are eliminated, whereas answers B, C, and E are still possibilities. Let’s now evaluate (2).
Although we may be tempted to immediately dismiss (2) for the same reason as (1), we should be careful because (2) presents slightly different information. As we can see from the above odd/even rules, multiplication with an even number will always result in an even number. The question, however, is whether (a + c) or (b + c) has to be even. Let’s try two cases:
| Case 1: | Let’s say that a and c are both even. Then we have (even + even) x (even + even) = (even) x (even) = even. So, answering the original question, do we have an even integer? YES |
| Case 2: | Since our first case yielded an even integer, we now want to check whether it’s possible to get an odd integer. This only happens if we have odd x odd. So how can we get odd times odd? What if a is even and c is odd. Then we have (even + odd) x (even + odd) = (odd) x (odd) = odd. So, answering the original question, do we have an even integer? NO |
Once again, we have a NO case and a YES case, so (2) is not sufficient. Using our answer elimination flowchart, we can now also eliminate answer B; answers C and E are still possibilities. Because neither (1) nor (2) is sufficient alone, we must evaluate (1) and (2) used together.
With an odd a and an even b, we have: (odd + c) x (even + c)
Since we don’t know about c, we should try two cases for c – odd and even:
| Case 1: | Let’s say that c is odd. Then we have (odd + odd) x (even + odd) = (even) x (odd) = even. So, answering the original question, do we have an even integer? YES |
| Case 2: | Let’s now say that c is even. Then we have (odd + even) x (even + even) = (odd) x (even) = even. So, answering the original question, do we have an even integer? YES |
In both possible cases, we can answer the original question with a YES. Since we have a definite answer to the original question (YES), statements (1) and (2) together are sufficient and we pick answer C.
Note that the above explanation takes the mathematical justification approach by using the odd/even rules. For this problem, we could have just as easily tried plugging in numbers. Let’s see how this would work in evaluating (1) and (2) together.
Since a is odd and b is even, let’s plug in simple numbers that meet those conditions: a = 1 and b = 2. We are told that a, b, and c are positive integers, so we cannot use zero or negative numbers. We should try two cases for c – odd and even:
| Case 1: | Let’s say that c = 3 (odd case). Then we have (1 + 3) x (2 + 3) = (4) x (5) = 20 = even. So, answering the original question, do we have an even integer? YES |
| Case 2: | Let’s now say that c = 4 (even case). Then we have (1 + 4) x (2 + 4) = (5) x (6) = 30 = even. So, answering the original question, do we have an even integer? YES |
As before, we can answer the original question with a YES in both cases, so we pick answer C.